Numerically Approximating Conformal Maps with the Zipper Algorithm

Update: A commenter points out some errors in the terminology used. Additionally, there are now much better codes available for zipper-like algorithms in Matlab, as well as Julia implementations.  Additionally there are codes for the circle packing algorithm which someone may find useful.

As with the previous post, I want to mention some other work I did related to my DPhil course. This project was about implementing an algorithm to numerically compute conformal maps between simply connected domains and the unit disk. By the Riemann Mapping Theorem we know that for every such domain, a map must exist, but finding it analytically is rarely easy if possible at all. A good discussion of these ideas can be found, for instance, in Terence Tao’s lecture notes on the subject. Given a domain, there are several ways to numerically construct a map which approximates the conformal map guaranteed by this Theorem, such as by approximating the domain by polygons and using Schwarz-Christoffel maps to map it to the unit disk.

I implemented the Geodesic or Zipper algorithm due to Don Marshall. The full code (in Matlab) can be found here, along with a few graphical tools to explore it. It has some precision problems for domains with “sharp” boundaries for the inverse map (that is, mapping the unit disk to a given domain) but overall I’m pretty happy with the results. I did not include all of the approximations one could to make the algorithm both more accurate and more efficient, but I may come back to this later and do that, as well as demonstrate some of the applications of these maps. If you’re interested, I would also check out this Thesis on the topic which I found to be useful. It also contains Python code for this algorithm as well as another approach using sphere packing. Below I will include a few examples of what this code can generate, but I encourage you to download it and play with it yourself. As always, comments and questions are appreciated!

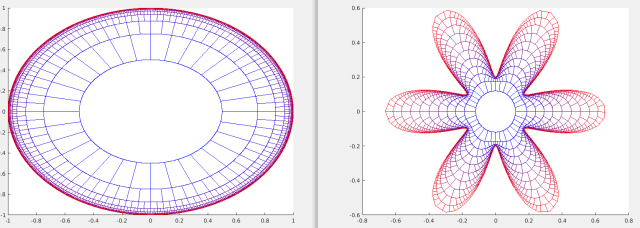
Here is an example map from a Carleson grid, where each successive circle has  additional lines and has a radius of . The domain is given by the polar function, .

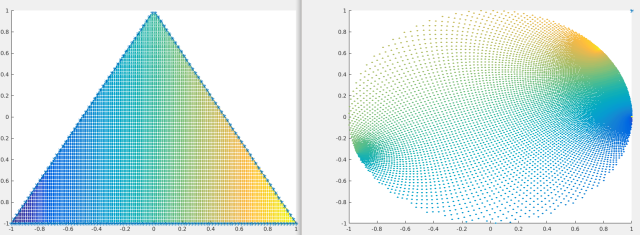
Here is an example of mapping a triangular domain to the unit disk.

Lastly, here is a mapping from a 4th-iteration Koch Snowflake to the unit disk.

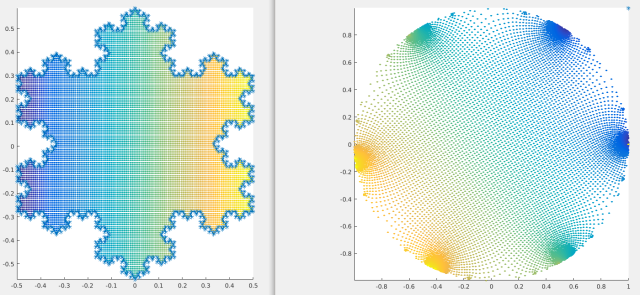
The inverse map for this domain has numerical problems as mentioned above. These could likely be remedied via various approximations that I may implement later.